Was sind Filter und wozu sind sie gut?
Filter werden in der Elektrotechnik immer da verwendet, wo die Eigenschaften von Signalen verändert werden sollen. Das könnte z.B. das reduzieren von Rauschen oder das Trennen von hohen und tiefen Frequenzen sein.
Filter können nicht dazu verwendet werden, um Informationen aus einem Signal zu bekommen, dass nicht schon vorher enthalten war.
Z.B. sind die Signale eines EKG meist von einem 50Hz Signal überlagert, dass vor der Weiterverarbeitung gefiltert werden muss.
Welche Filter gibt es?
Der Tiefpass (1. Ordnung):
Als Tiefpass bezeichnet man Filter, die Signalanteile mit Frequenzen unterhalb ihrer Grenzfrequenz passieren lassen, Anteile mit höheren Frequenzen dagegen dämpfen.
Das Schaltbild des Tiefpass-Filters sieht wie folgt aus:
Der Hochpass (1. Ordnung)
Als Hochpass bezeichnet man Filter, die Signalanteile mit Frequenzen über ihrer Grenzfrequenz passieren lassen, Anteile mit tieferen Frequenzen dagegen dämpfen.
Das Schaltbild des Hochpass-Filters sieht wie folgt aus:
Es gibt auch noch eine Reihe anderer Filter wie z.B. den Bandpass-Filter oder den Kalman-Filter, etc. auf die ich hier aber nicht weiter eingehen werde. Bleiben wir also bei den Basics.
Die Grenzfrequenz
Filter wie der Tiefpass oder der Hochpass haben eine Grenzfrequenz. Diese Grenzfrequenz entspricht der der Frequenz, ab der die Amplitude des Ausgangs-Signals auf einen Wert von -3dB der Amplitude des Eingangs-Signals abfällt.
Die Formel zur Berechnung der Grenzfrequenz in einem Tiefpass und einem Hochpass ist die gleiche. Der Unterschied besteht darin, dass bei einem Hochpass die tiefen Frequenzen gefiltert werden und bei den Tiefpass die hohen.
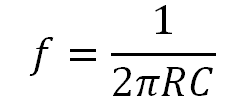
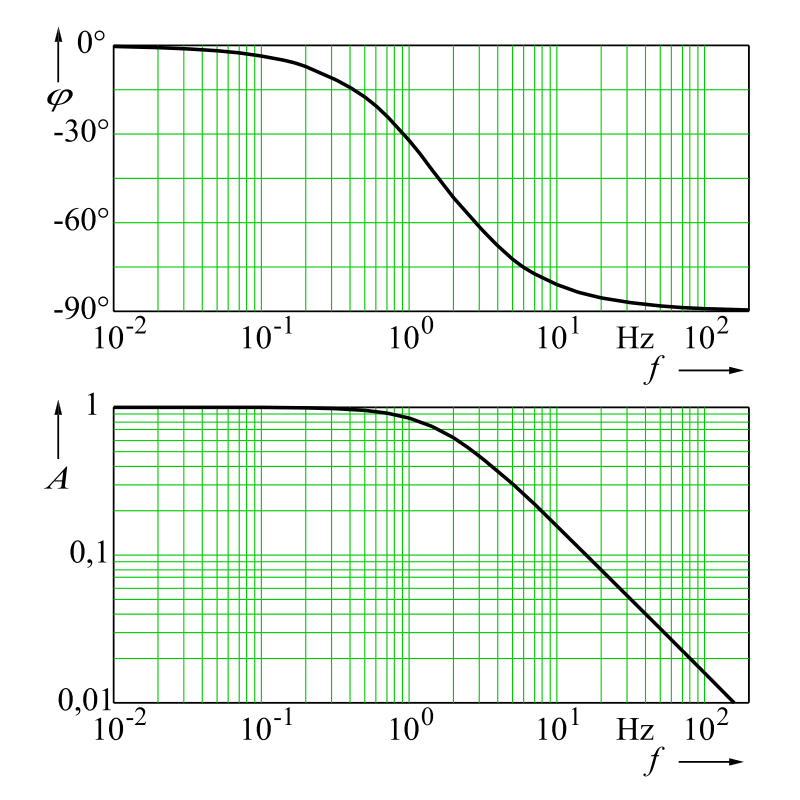
Quelle: https://de.wikipedia.org/wiki/Tiefpass#/media/Datei:Bodediagramm_Tiefpass.svg
Hochpass-Filter & Tiefpass-Filter pragmatisch programmieren
Das Programmieren eines solchen Filters ist relativ komplex und von weiteren Faktoren wie der Sampling Rate, aber es gibt eine einfache Abkürzung, bei der man nur wenig Mathematik benötigt, dafür aber ein wenig herumprobieren muss. Die Formeln für die Filter sind sehr einfach und es gilt nur den Wert für filterValue zwischen 0 und 1 durch ausprobieren herausfinden.
Der Tiefpass-Filter
float filterValue = 0,9 // Wert zwischen 0 und 1 (0 = kein Filter | 1 = alles weggefiltert)
float gefiltertestSignal = 0;
gefiltertestSignal = eingangsSignal * (1- filterValue) + gefiltertestSignal * filterValueDer Hochpass-Filter
float filterValue = 0,9 // Wert zwischen 0 und 1 (0 = kein Filter | 1 = alles weggefiltert)
float gefiltertestSignal = 0;
float filterHelper = 0
filterHelper = eingangsSignal * filterValue + filterHelper * (1- filterValue)
gefiltertestSignal = eingangsSignal – filterHelper;Ich habe die Formeln mal in einer „Google Tabellen“ Mappe abgelegt und ein wenig damit herumgespielt. In der ersten Spalte wird eine Zahl von 0 – x hochgezählt. In der zweiten Spalte wird ein Sinus berechnet, der in dem ersten Diagramm angezeigt wird.
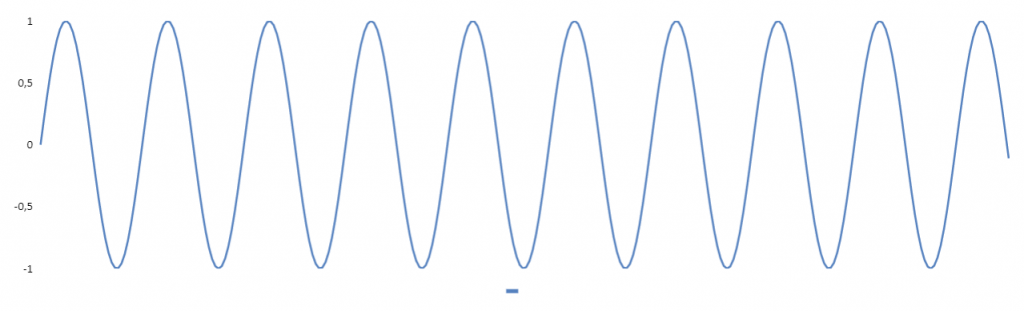
In der dritten Spalte wird ein zufälliges hochfrequentes Rauschen hinzugefügt.
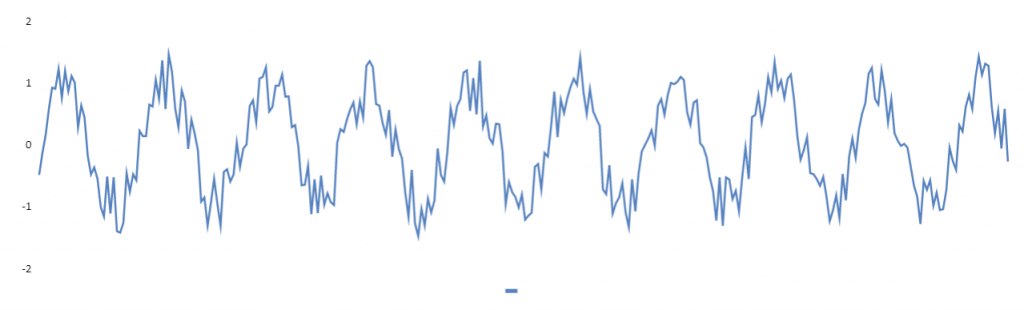
Danach bekomme das Signal noch eine niederfrequente Überlagerung
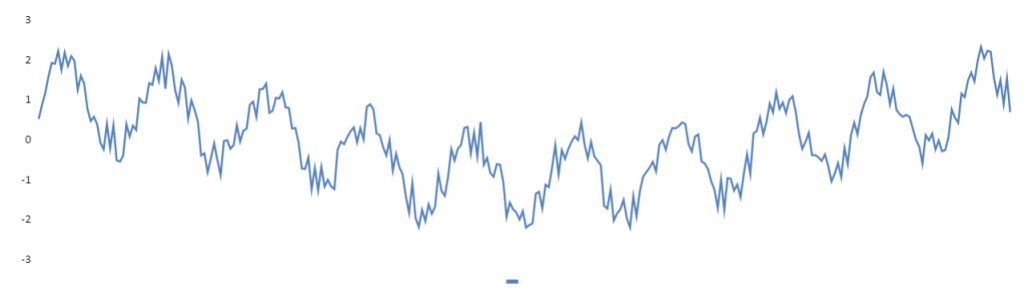
Damit ist das Eingangssignal so weit vorbereitet. Es besteht nun aus einem Sinus, einem hochfrequenten Rauschen und einer niederfrequenten Überlagerung. Also ideal um mit einem Hochpass-Filter und einem Tiefpass-Filter das ursprüngliche Sinus Signal wieder herzustellen.
Schritt 1: der Tiefpass Filter:
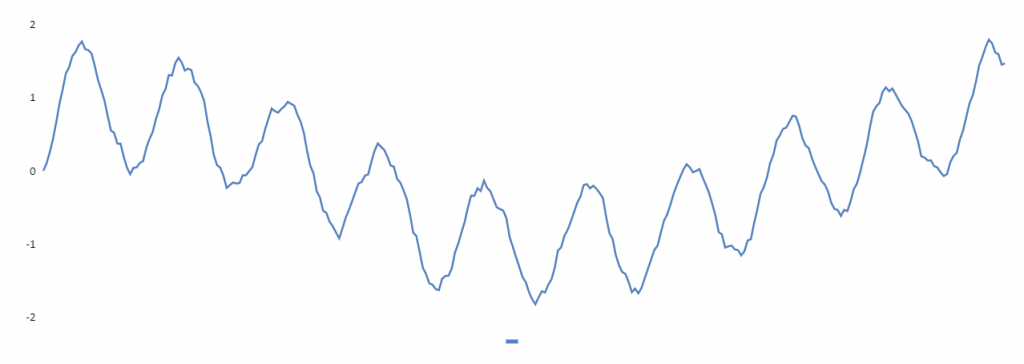
In Spalte E ist ein Tiefpass mit folgender Formel realisiert.
=(D3$E$2)+(E3(1-$E$2))
Das Ergebnis kann sich fast schon wieder sehen lassen. Das hochfrequente Rauschen hat der Tiefpass-Filter gut unter Kontrolle bekommen.
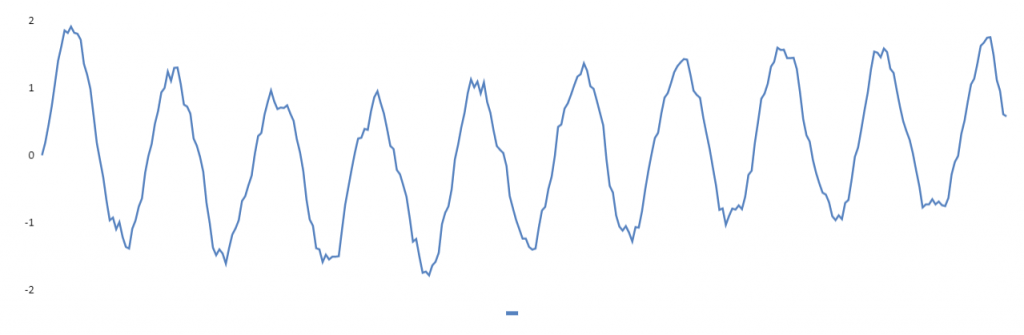
Zu guter Letzt noch der Hochpass-Filter mit dem die niederfrequente Überlagerung aus dem Signal gefiltert werden soll. Hierfür verwende ich 2 Spalten. Der filterHelper ist in Spalte G definiert =($G$2E4)+((1-$G$2)G3) und in Spalte F wird dann das gefilterte Signal mit =(E4-G4)*2 berechnet und noch mal 2 multipliziert (eigentlich überflüssig, aber sehe es mal als kleine Endstufe ? ).
Vergleicht man das Ergebnis mit dem ursprünglichen Sinus Signal, sieht man noch ein paar Reste der künstlich erzeugten Störungen. Wenn man genau hinschaut, kann man auch eine leichte Phasenverschiebung erkennen, die typisch für RC-Filter ist (https://de.wikipedia.org/wiki/Phasenverschiebung).
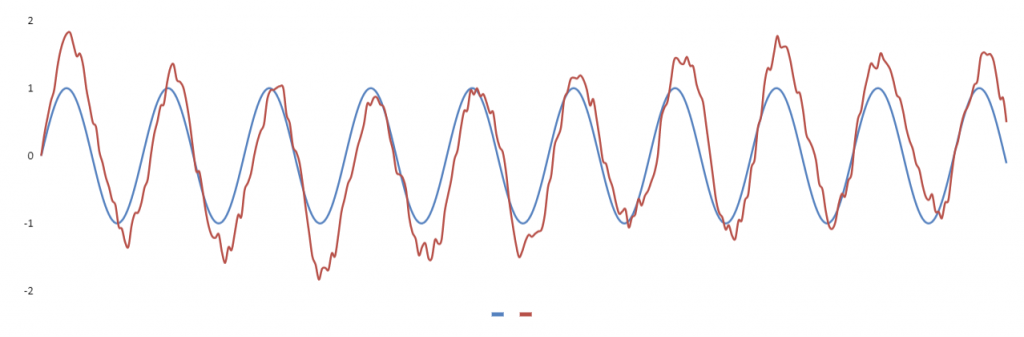
Alles in allem hat der Filter aber schon ganz gute Arbeit geleistet und den größten Teil der Störungen entfernt.
Das Spreadsheet kann hier in Google Docs geöffnet werden:
https://docs.google.com/spreadsheets/d/1Oc4rG7s6tWax0PZcAznaUasG9ex6qHq0ekxvli1ZM0I/edit?usp=sharing
Einfach mal in der Zeile die ich grün markiert habe ein wenig herumspielen. Hier können Frequenzen, Amplituden und Stärke der Filter eingestellt werden.
B2 = Verändert die Frequenz des Ursprungssignals
C2 = Anpassung der Amplitude des Rauschend
D2 = Verändert die Frequenz der niederfrequenten Überlagerung
E2 = Stärke des Tiefpass-Filters (0-1)
G2 = Stärke des Hochpass-Filters (0-1)
Tiefpass für Arduino IDE
/*
* Tiefpass Filter Code für die Arduino IDE
*/
float filterValue = 0.9; // Wert zwischen 0 und 1 (0 = kein Filter | 1 = alles weggefiltert)
float gefiltertestSignal = 0;
float eingangsSignal = 0;
void setup() {
// put your setup code here, to run once:
}
void loop() {
eingangsSignal = 0; // TODO
gefiltertestSignal = eingangsSignal * (1- filterValue) + gefiltertestSignal * filterValue;
}Hochpass für Arduino IDE
/*
* Hochpass Filter Code für die Arduino IDE
*/
float filterValue = 0.9; // Wert zwischen 0 und 1 (0 = kein Filter | 1 = alles weggefiltert)
float gefiltertestSignal = 0;
float filterHelper = 0;
float eingangsSignal = 0;
void setup() {
// put your setup code here, to run once:
}
void loop() {
eingangsSignal = 0; // TODO
filterHelper = eingangsSignal * filterValue + filterHelper * (1- filterValue);
gefiltertestSignal = eingangsSignal - filterHelper;
}Natürlich kann man diese Filter auch kaskadieren, um noch stärker zu filtern. Allerdings sollte man es hier nicht übertreiben, sonst bleibt am Ende nichts mehr vom ursprünglichen Signal übrig.